Para continuar con nuestro proyecto vamos a hacer un estudio aplicando teoría de grafos y de redes complejas con el objetivo de demostrar si las redes de bicicletas pueden asemejarse a una red compleja o no. Para el análisis estructural de la red, necesitaremos calcular algunos atributos como:
- Número total de aristas.
- Secuencia de grados.
- Grado medio.
- Distribución de probabilidad de los grados.
- Camino mínimo entre dos nodos.
- Distancia, longitud promedio de caminos y diámetro del grafo.
- Número de agrupaciones conexas.
- Coeficiente de agrupamiento.
- Transitividad.
Empezaremos explicando la estructura de datos que almacenará el grafo y luego los métodos que calculan estos atributos.
ESTRUCTURA DE DATOS
La estructura que usaremos para almacenar un grafo será una matriz de adyacencia de dimensiones NxN siendo N el número de nodos del grafo.
- Cada posición (j,i) de la matriz tendrá un valor numérico (peso) que será infinito cuando no haya arista entre los nodos j e i. Si el grafo es no pesado, los valores posibles serán 1 o infinito y si es pesado, podrán contener cualquier valor mayor que 0 (no consideramos pesos negativos).
- No se considerarán lazos, es decir, aristas que tengan origen y destino en el mismo nodo.
Un ejemplo de grafo dirigido no pesado podría ser el siguiente:
NÚMERO TOTAL DE ARISTAS
El cálculo del número de aristas consiste contar cuántas celdas de la matriz de adyacencia almacenan un valor distinto a infinito. En caso de que el grafo sea no dirigido, debemos tener en cuenta que hay que dividir el valor resultante a la mitad. El código que usaría un grafo dirigido es:
SECUENCIA DE GRADOS
El grado de un nodo es el número de aristas en las que participa. Si el grafo es dirigido, distinguimos entre grado entrante (número de aristas en las que el nodo participa como destino) y grado saliente (número de aristas en las que el nodo participa como origen). La secuencia de grados es la lista que contiene los grados de todos los nodos de la red. Si grafo es dirigido, tenemos que diferenciar entre secuencia de grados entrante y secuencia de grados saliente. Si el grafo es no dirigido, las secuencia entrante y saliente coinciden.
El código que hace esto es:
El código que hace esto es:
GRADO MEDIO
El grado medio es la sumatoria de la secuencia de grados entre el número de nodos del grafo. Si grafo es dirigido, tendremos que diferenciar entre grado medio entrante y grado medio saliente. El código que calcula esto es:
DISTRIBUCIÓN DE PROBABILIDAD DE LOS GRADOS
La distribución de probabilidad de los grados es una lista que contiene en la posición i-ésima la probabilidad de que un nodo de la red escogido al azar sea de grado i. Podemos hacer el cálculo como si estuviéramos haciendo un histograma de frecuencias y después dividir cada posición por el número de nodos de la red. El código en cuestión es:
CAMINO MÍNIMO ENTRE DOS NODOS
El camino entre dos nodos j e i se define como la secuencia de nodos/aristas que hay que visitar para llegar desde el nodo j al i. El camino mínimo será aquel que visite menos nodos/aristas. Para calcular el camino entre cada par de nodos del grafo, hemos implementado el algoritmo de Floyd.
Se trata de un algoritmo que utiliza dos matrices como memoria dinámica. Una matriz se usa para determinar cuál es el coste mínimo entre dos nodos (la llamaremos D de distancia) y otra para la secuencia de nodos que se deben visitar para ir de uno a otro (la llamaremos C de camino).
En la Wikipedia podéis obtener más datos sobre el algoritmo, incluso un pseudocódigo, un código en C++ y Java y una traza de ejecución. (enlace).
DISTANCIA, LONGITUD PROMEDIO DE CAMINOS Y DIÁMETRO DE UNA RED
Los tres conceptos que presentamos ahora están muy relacionados entre ellos y se apoyan todos en el cálculo de camino mínimo entre dos nodos de la red:
- La distancia entre dos nodos es la longitud del camino mínimo entre ambos.
- La longitud promedio es el promedio de las distancias más pequeñas entre cualquier par de nodos de la red.
- El diámetro de la red es el máximo de las distancias más cortas entre cualquier par de nodos de la red.
En nuestro código, para obtener estos atributos, solo tendremos que consultar la matriz D (la definimos antes como la matriz que contiene el coste mínimo de camino entre cada par de nodos de la red).
Para la distancia entre dos nodos, solo tenemos que indexar en la matriz D, para la longitud promedio, hacemos el promedio de los valores de D y para el diámetro de la red, buscamos el máximo valor de D.
El código de la longitud promedio será:
Y el del diámetro de la red:
NÚMERO DE AGRUPACIONES CONEXAS
Una agrupación conexa es un subconjunto de los nodos donde cada nodo está conectado al menos a otro nodo del subconjunto. La forma de calcularlo consiste en considerar inicialmente que todos los nodos están desconectados e ir agrupando en base a los vecinos de cada nodo. El código que permite hacer esto es el siguiente:
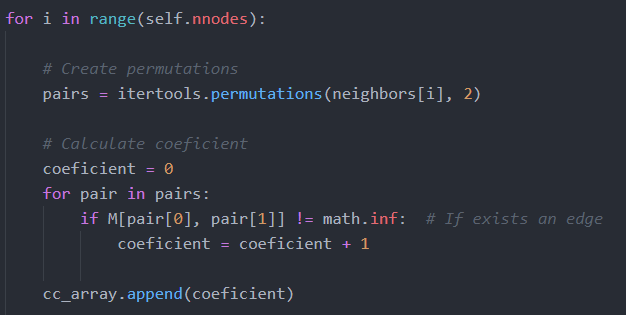
COEFICIENTE DE AGRUPAMIENTO
Es una medida del grado en el que los nodos de una red tienden a agruparse entre ellos. El coeficiente de agrupamiento del nodo i-ésimo se calcula como el número de pares (l,m) de nodos vecinos de i conectados por aristas dividido por el número total de pares que podrían existir de nodos vecinos de i. En definitiva, se puede asimilar al número de triángulos que se pueden formar con el nodo i.
A modo de ejemplo, vamos a mostrar un grafo con los triángulos que se pueden formar en él.
Los triángulos se forman considerando aristas dirigidas, es decir, si hay dos aristas entre dos nodos, como ocurre entre el nodo 4 y 2, se contabiliza como dos triángulos. Los triángulos para este grafo son:
El código que permite hacer este cálculo es:
TRANSITIVIDAD
También se puede llamar como coeficiente de agrupamiento global y se calcula como el número de triángulos que existen en la red dividido por el número de tripletes. Un triplete es un subgrafo con tres nodos y dos aristas.
El número de triángulos se puede calcular como:
El número de tripletes se puede obtener como:
Una vez tenemos todos estos atributos, podremos empezar nuestro análisis estructural. En los siguiente post, pondremos a prueba algunas propiedades de redes complejas y redes aleatorias y aplicaremos los mismos tests sobre nuestras redes de bicicletas.